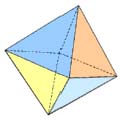
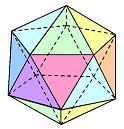
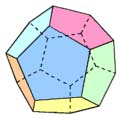
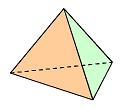
regelmatig veelvlak:

Een regelmatig veelvlak of platonisch lichaam is een veelvlak dat begrensd wordt door congruente regelmatige veelhoeken. Elk hoekpunt van het veelvlak moet tot evenveel zijvlakken behoren. Er bestaan vijf soorten regelmatige veelvlakken: de tetraëder (viervlak), de kubus (zesvlak), de octaëder (achtvlak), de dodecaëder (twaalfvlak), en de icosaëder (twintigvlak).
De Griekse filosoof Plato beschreef deze vijf lichamen al in het jaar 350 voor Christus.

viervlak (piramide)        zesvlak                 achtvlak               twaalfvlak          twintigvlak

Waarom maar vijf regelmatige veelvlakken?

Dit hangt samen met het aantal zijvlakken dat in hetzelfde hoekpunt samenkomt.
De som van de hoeken daar moet kleiner zijn dan 360º, want anders zouden de zijvlakken in hetzelfde vlak liggen (of "uitsteken").
Verder moeten in elk hoekpunt minstens 3 vlakken samenkomen. Elke vlakhoek moet dus kleiner zijn dan 360°/3 = 120°.
Er komen dus slechts drie-, vier- en vijfhoeken als zijvlak in aanmerking.
De hoek van een vijfhoek is gelijk aan 108°. Vier zijvlakken met een vijfhoek kan niet.
Er is dus slechts 1 regelmatig veelvlak (mogelijk) met een vijfhoek als "bouwsteen".
De hoek van een vierkant is 90º. Ook hier zijn vier zijvlakken onmogelijk.
Er is dus slechts 1 regelmatig veelvlak (mogelijk) met een vierkant als "bouwsteen".
Voor de driehoek hebben we:
3 x 60 = 180º; 4 x 60 = 240º; 5 x 60 = 300º.
Er zijn dus 3 regelmatige veelvlakken (mogelijk) met een driehoek als "bouwsteen".
En dat deze vijf er inderdaad ook zijn, zien we hierboven.

http://www.kennislink.nl/web/show?id=119916
~http://mediatheek.thinkquest.nl/~kla046/platonisch.htm
http://www.fi.uu.nl/toepassingen/00297/toepassing_wisweb.html

In de tijd van de Duitse astronoom Johannes Kepler (1571-1630) waren vijf planeten bekend. Kepler kwam op het idee dat de bouw van het planetenstelsel in verband moest staan met de vijf regelmatige veelvlakken. Hij beschreef dat als volgt: wanneer men op de cirkelbanen van de opeenvolgende planeten bollen construeert, dan past tussen elke twee opeenvolgende bollen een regelmatig veelvlak zo, dat de zijvlakken van dit veelvlak de binnenste bol raken en zijn hoekpunten op de buitenste bol liggen. Hij plaatste hierbij van binnen naar buiten: achtvlak, twintigvlak, twaalfvlak, viervlak en zesvlak.

http://nl.wikipedia.org/wiki/Mysterium_Cosmograficum